 Euler Angles
Euler Angles Filenames
Filenames Logical access
Logical access Image center
Image center Physical access
Physical access Euler Angles
Euler Angles Filenames
Filenames Logical access
Logical access Image center
Image center Physical access
Physical access
 Euler Angles
Euler AnglesGraphical InterpretationBack to the beginning
To know more about Euler angles
To know even more
 Filenames
Filenames| Data type | Suggested extension | Suggested filenames |
| Images | .xmp | g1ta00001.xmp |
| Volumes | .vol | art00001.vol, wbp00001.vol, sirt00001.vol |
| Volumes | .xmp | art00001.xmp, wbp00001.xmp, sirt00001.xmp |
| Selection Files | .sel | g1t.sel |
| Document Files | .xmp | angles.xmp |
Notice also that Spider requires all data files (volumes, images, document files, ...) to have the same extension. You might prefer this other convention if you don't want to make copies of the files, or to have to rename the files before entering in Spider.
 Logical
access
Logical
accessSuppose now that we are interested to have the logical origin at the center of the image 65x65, ie, at physical position [32][32]. This would mean that the physical position [0][0] is now at logical position (-32,-32), and the logical indexes range now from -32 to 32.
This logical index defintion is done by means of the starting indexes
of matrices (see matrix2D) where you can define which logical position
is occupying the first physical pixel, ie,
I().startingY()=-32;
I().startingX()=-32;
From now on you can start to access to logical positions even with negative
indexes. The usual way of establishing loops inside this logical images
is by using the starting and finishing information of its axes
Image I(65,65);
I().init_random();
float sum=0;
for (int i=STARTINGY(I()); i<=FINISHINGY(I()); i++)
for (int j=STARTINGX(I()); j<=FINISHINGX(I()); j++) {
sum += I(i,j);
// sum += IMGPIXEL(i,j);
}
Although the previous example has been used using the class Image, the
logical access rely on the classes matrix1D, matrix2D, and matrix3D, and
all the concepts explained for images are extensible for vectors and volumes.
The related functions are STARTINGX, STARTINGY, STARTINGZ,
FINISHINGX, FINISHINGY, FINISHINGZ, IMGPIXEL, DIRECT_IMGPIXEL, VOLVOXEL,
DIRECT_VOLVOXEL, VEC_ELEM, MAT_ELEM, VOL_ELEM, DIRECT_VEC_ELEM, DIRECT_MAT_ELEM,
DIRECT_VOL_ELEM
Pay attention to the index order when pointing to a pixel, first you have to give the most outer coordinate (which is the less varying one in the actual implementation), and then increase the coordinate. For volumes the usual way of making a loop is
Volume V(65,65,65);
V().init_random();
float sum=0;
for (int k=STARTINGZ(V()); k<=FINISHINGZ(V()); k++)
for (int i=STARTINGY(I()); i<=FINISHINGY(I()); i++)
for (int j=STARTINGX(I()); j<=FINISHINGX(I()); j++) {
sum +=V(k,i,j);
}
Notice that if you don't modify the origin of the multidimensional array
then the physical and logical accesses are the same.
 Image
center
Image
center
This means that for images with an even dimension, the center will be "displaced" in that direction. Let's have a look on the following two diagrams of cell indexes.
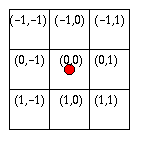
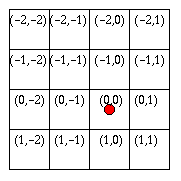
For volumes the idea is more or less the same. The benefit from this origin choice is that the origin is always at a pixel point, but as a disadvantage the volume might not be symmetrical with respect to the center.
 Physical
access
Physical
access
Regarding the physical origins and axis directions, the convention used is the following
For Vectors: (0) index at the left of the vector
For Matrices: (0,0) index at the top-left corner of the matrix
For Volumes: (0,0,0) index at the rear-top-left corner of the volume
Physical loops are based on a different set of functions than logical ones. For instance the former sum of image values could be rewritten in a physical fashion (but remember always that the logical access is preferred).
Image I(65,65);
I().init_random();
float sum=0;
for (int i=0; i<=YSIZE(I()); i++)
for (int j=0; j<=XSIZE(I());
j++) {
sum +=DIRECT_IMGPIXEL(I,i,j);
}
